空间滤波
空间滤波机理
滤波是指接收或拒绝一定的频率分量。一般来说,使用大小为m x n的滤波器对大小为M x N的图像进行线性空间滤波,有以下公式:
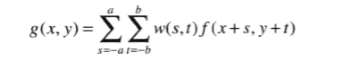
其机理为:
空间相关与卷积的区别:

平滑空间滤波器
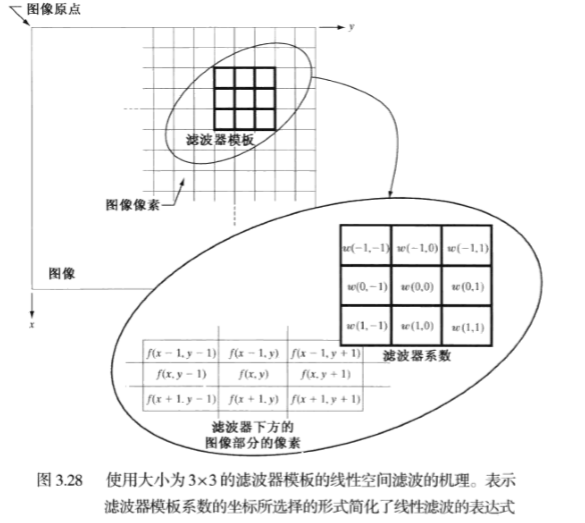
有平滑线性滤波器和统计排序滤波器(非线性)。平滑线性滤波器也称为均值滤波器,其滤波模板如下所示:
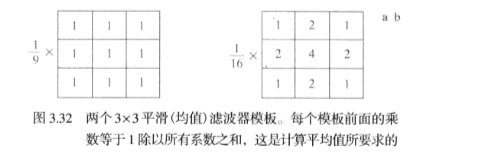
则其运用为:

- task3_05:
- 编写程序以执行图像的空间过滤,可以将空间过滤模板的大小固定为3 x 3。
- 滤波系数必须是可以输入到程序中的变量。
实现代码:
import cv2
import numpy as np
import matplotlib.pyplot as plt
def filter_test(img,wx,m,n):
m = m // 2
n = n // 2
h = img.shape[0]
w = img.shape[1]
newImg = np.zeros((h,w,3),np.float64)
for i in range(h): # 按照公式进行滤波处理
for j in range(w):
t = np.zeros((1,1,3),np.float64)
for a in range(-1*m,m+1):
for b in range(-1*n,n+1):
if 0 <= i + a < h and 0 <= j + b < w: # 判断索引值是否可用
t += img[i+a,j+b]*wx[a,b]
newImg[i,j] = t
newImg = np.uint8(newImg)
return newImg
img = cv2.imread(r"D:\JupyterStore\zdip\t3_05.tif")
wx = np.array([[1/9,1/9,1/9],[1/9,1/9,1/9],[1/9,1/9,1/9]])
img_test = filter_test(img,wx,3,3) # 显然这里采取的是3*3均值滤波
plt.figure("0")
plt.imshow(img)
plt.figure("1")
plt.imshow(img_test)
实现效果:
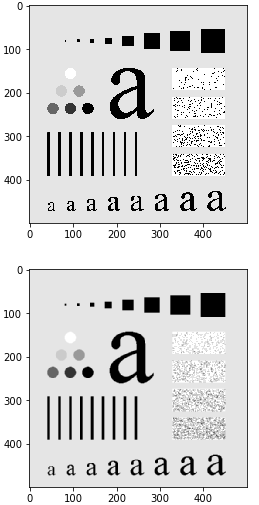
可以观察到,原图像的边缘锯齿化非常严重,而处理过的图像在其边缘锯齿上起到了平滑化的效果。同时对比右边的四块带点区域,可以发现图片细节有些许丢失。
锐化空间滤波器
一般的处理方法是用二阶微分的拉普拉斯算子来进行图像锐化。我们将二阶微分定义为差分:
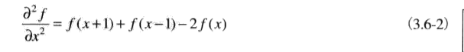
而拉普拉斯算子连续表达式
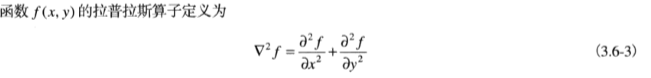
则可得到离散的拉普拉斯算子表达式:
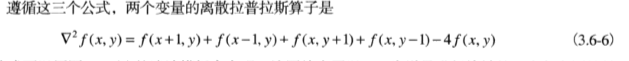
最终得到在进行图像增强时用到的式子:

task3_06:使用上一个task中的程序来实现结合等式所述的拉普拉斯增强技术。公式(3.6-7)。
实现代码:
import cv2
import numpy as np
import matplotlib.pyplot as plt
def filter_test(img,wx,m,n):
m = m // 2
n = n // 2
h = img.shape[0]
w = img.shape[1]
newImg = np.zeros((h,w,3),np.float64)
for i in range(h): # 按照公式进行滤波处理
for j in range(w):
t = np.zeros((1,1,3),np.float64)
for a in range(-1*m,m+1):
for b in range(-1*n,n+1):
if 0 <= i + a < h and 0 <= j + b < w: # 判断索引值是否可用
t += img[i+a,j+b]*wx[a,b]
newImg[i,j] = t
newImg = np.uint8(newImg)
return newImg
img = cv2.imread(r"D:\JupyterStore\zdip\t3_06.tif")
wx = np.array([[0,1,0],[1,-4,1],[0,1,0]])
img_test = filter_test(img,wx,3,3)
plt.figure("0")
plt.imshow(img)
plt.figure("1")
plt.imshow(img_test)
效果如下:
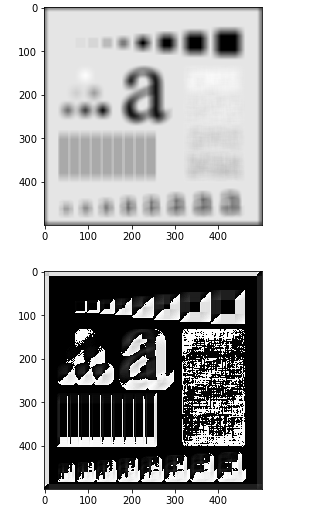
非锐化屏蔽
其理论操作步骤为:
- 模糊原图像
- 从原图像中减去模糊图像(产生的差值图称为模板)
- 将模板加到原图像上