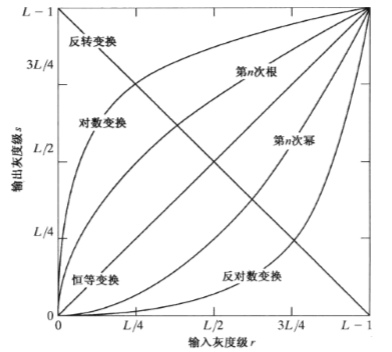
灰度变换
灰度变换函数
r,s分别代表处理前后的像素值。包括图像反转、对数变换、幂律变换、分段线性变换函数。
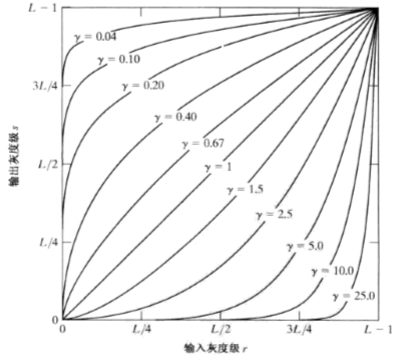
这里要注意对数变换和幂律变换的常数取值,下图分别为对数变换、幂律变换常数变化曲线图。
- task3_01:对原始数字乳房X射线照片进行图像反转,观察其效果。
代码实现:
import cv2
import matplotlib.pyplot as plt
img = cv2.imread(r"D:\JupyterStore\zdip\t3_01.tif")
plt.figure("1")
plt.imshow(img)
# 灰度反转 s=L-1-r 图像灰度级范围为[0,L-1]
for i in range(0,img.shape[0]):
for j in range(0,img.shape[1]):
img[i][j] = 255 - img[i][j]
plt.figure("2")
plt.imshow(img)
实现效果:
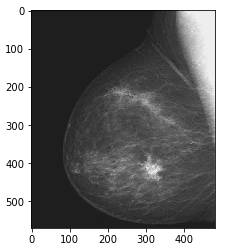
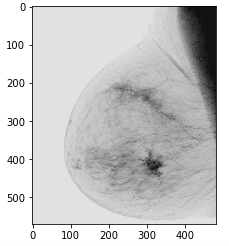
实现现象:可以看到,反转后的图片在纹理上更加清晰,这样做的原因是原图灰度分布偏黑色,不怎么好区分,而将图片反转后,色彩也发生了变化,原本黑色的部位变亮了,这样方便对图像内部细节的进一步研究。
-
task3_02:
使用强度变换的图像增强。该任务的重点是尝试强度转换以增强图像,使用以下相应方法对图片进行增强。
- 对数的对数变换(3.2-2)
- 幂律变换(3.2-3)
tips:公式如下
代码实现:
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread(r"D:\JupyterStore\zdip\t3_02.tif")
plt.figure("1")
plt.imshow(img)
# 对数变换 这里常数c取了47
img_log = 47*np.log(img + 1)
img_log = np.uint8(img_log + 0.5)
plt.figure("2")
plt.imshow(img_log)
# 幂次变换 常数取了 32/0.4
img_gama = 32*np.power(img,0.4)
img_gama = np.uint8(img_gama + 0.5)
plt.figure("3")
plt.imshow(img_gama)
实现效果:依次为原图、对数变换图、幂次变换图


现象观察:可以看到对数和幂次变换的处理效果都不错,这里注意的是常数c和y的取值,不同的值是会产生不同的效果,所选取的值是在多次测试后,人为选定比较好的数据点。
直方图处理
图像灰度直方图类似我们之前task2_01做过的统计。每一灰度级数所占的像素个数n,n/r*c就是归一化后的直方图,其中r,c分别为高宽。rc相乘即为像素总个数。
直方图均衡处理,有:

直方图规定化,有:

其中两个公式分别是:
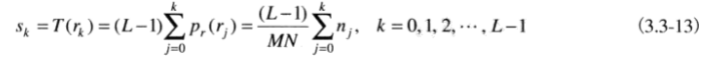

- task3_03:编写用于计算图像直方图的程序,实施第直方图均衡技术并对图片进行直方图均衡化。
tips:
- 样图采用比较大,1.44MB,处理时间可能久一点。
- 从原图到均衡处理后图片的映射需要注意其处理方式。
代码实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pylab
pylab.rcParams['figure.figsize'] = (10.0,6.0)
def histogram_test(img):
h = img.shape[0]
w = img.shape[1]
newImg = np.zeros((h,w,3),np.uint8)
sd = np.zeros(256) # 原始图像归一化直方图
hd = np.zeros(256) #均衡化后图像归一化直方图
imap = np.zeros(256) # 映射表
for i in range(h):
for j in range(w):
sd[img[i][j]] += 1
sd = sd / (h*w)
plt.figure('1')
plt.subplot(1,2,1)
plt.imshow(img)
plt.subplot(1,2,2)
plt.plot(sd)
plt.show()
#这里构造的是一个累加,i[0,256],j[0,i]
for i in range(256):
for j in range(i + 1):
imap[i] += sd[j]
imap[i] = round(imap[i] * 255) # 这里的255代表公式中的L-1
# 进行映射
for i in range(h):
for j in range(w):
newImg[i][j] = imap[img[i][j]]
for i in range(h):
for j in range(w):
hd[newImg[i][j]] += 1
hd = hd / (h*w)
plt.figure('2')
plt.subplot(1,2,1)
plt.imshow(newImg)
plt.subplot(1,2,2)
plt.plot(hd)
plt.show()
if __name__ == '__main__':
img = cv2.imread(r"D:\JupyterStore\zdip\t3_04.jpeg")
histogram_test(img)
实现效果:
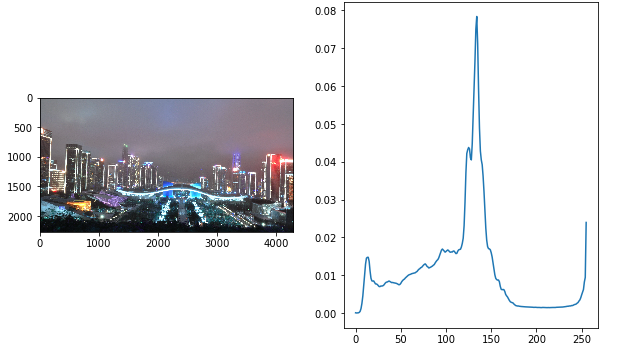
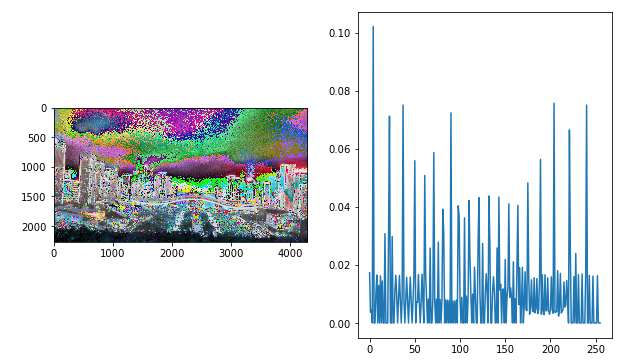
效果观察:可以看到均衡化后的图像直方图较原图像直方图更为均匀,但这幅全景图均衡化的效果并不是很好,图像色彩失真。

