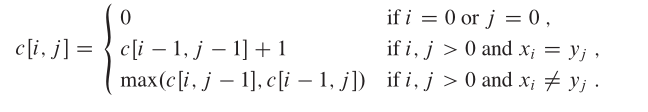动态规划
记忆化
- 裴波那契数列:
- 1、1、2、3、5、8、13、21、34、……
- 以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
- 实现:
#include <iostream>
using namespace std;
// 迭代版裴波拉契数列
int toFib(int n){
int f = 1; int g = 0;
while(0 < n--){
g = g + f;
f = g - f;
}
return g;
}
int main()
{
int f1 = toFib(6);
cout << "裴波拉契数列第6项是:" << f1 << endl;
}
- 控制台输出:
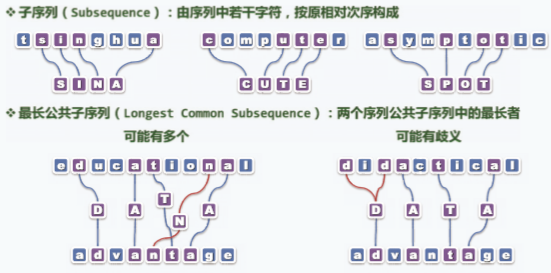
最长公共子序列
- 在处理最长公共子序列中出现的情况:


- 分别采用递归和迭代来分析问题:
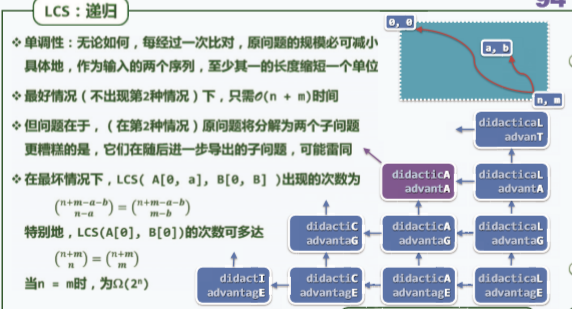
- 递归:
- 迭代:

-
借鉴学习
当然,这个概念讲的并不算非常清楚,所以找到了一篇解析比较详细的博文参考资料
下面给出最长公共子序列的实现代码:
- 基本递归版
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
char x[N],y[N];
int dp[N][N];
int b[N][N];
void Print(int i,int j)
{
// 见下图中的解释
if(i==0||j==0) // 递归终止条件
{
return ;
}
if(b[i][j]==1)
{
Print(i-1,j-1);
printf("%c",x[i-1]);
}
else if(b[i][j]==2)
{
Print(i-1,j);
}
else if(b[i][j]==3)
{
Print(i,j-1);
}
}
int main()
{
int lena,lenb,i,j;
while(scanf("%s%s",x,y)!=EOF)
{
// memset函数给内存赋值,这里起初始化全0的作用
memset(dp,0,sizeof(dp));
memset(b,0,sizeof(b));
lena=strlen(x);
lenb=strlen(y);
for(i=1;i<=lena;i++)
{
for(j=1;j<=lenb;j++)
{
// 第二种判断情况
if(x[i-1]==y[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
b[i][j]=1; // 来自于左上方
}
// 第三种判断情况
else
{
if(dp[i-1][j]>dp[i][j-1])
{
dp[i][j]=dp[i-1][j];
b[i][j]=2; // 来自于左方
}
else
{
dp[i][j]=dp[i][j-1];
b[i][j]=3; // 来自于上方
}
}
}
}
printf("最长公共子序列长度为:%d\n",dp[lena][lenb]);
printf("最长公共子序列为:");
Print(lena,lenb);
}
return 0;
}
对应上述的判断情况:
实现效果:
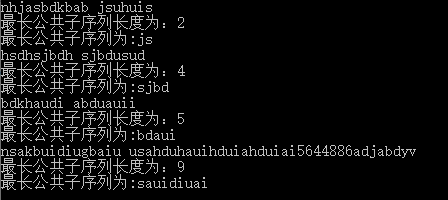
- 迭代版本
#include<stdio.h>
#include<string.h>
#include<stack>
#include<algorithm>
using namespace std;
#define N 1010
int dp[N][N];
char c;
int main()
{
char a[N];
char b[N];
scanf("%s%s",a,b);
int la=strlen(a);
int lb=strlen(b);
memset(dp,0,sizeof(dp));
for(int i=1; i<=la; i++)
{
for(int j=1; j<=lb; j++)
{
if(a[i-1]==b[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
int i=la,j=lb;
stack<char>s;
while(dp[i][j])
{
if(dp[i][j]==dp[i-1][j]) // 来自于左方向
{
i--;
}
else if(dp[i][j]==dp[i][j-1]) // 来自于上方向
{
j--;
}
else if(dp[i][j]>dp[i-1][j-1]) // 来自于左上方向
{
i--;
j--;
s.push(a[i]);
}
}
printf("最长公共子序列为:");
while(!s.empty())
{
c=s.top();
printf("%c",c);
s.pop();
}
return 0;
}
实现效果: