迭代与递归
减而治之
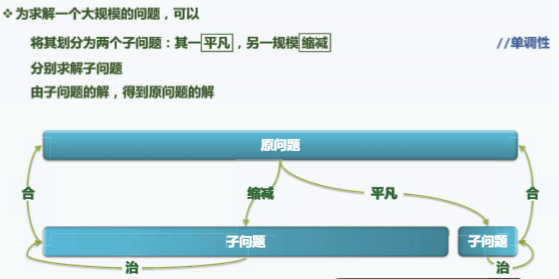
- 实现的几个例子:
#include <iostream>
using namespace std;
// 迭代求和
int mySum(int a[], int n){
int sum = 0;
for(int i=0; i<n; i++){
sum += a[i];
}
return sum;
}
// 递归求和
int toSum(int a[], int n){
return n < 1 ? 0 : toSum(a,n-1) + a[n-1];
}
// 迭代反转
void myReverse(int a[],int lo,int hi){
while(lo<hi){
swap(a[lo++],a[hi--]);
}
}
// 递归反转
void toReverse(int a[],int lo,int hi){
if(lo<hi){
swap(a[lo],a[hi]);
toReverse(a,lo+1, hi-1);
}
}
int main()
{
int A[15]={1,2,3,4,5,6,7,8,9};
cout << "原数列为:" << endl;
for(int j=0;j<9;j++)
cout << A[j] <<" ";
cout << "" << endl;
int sum1 = mySum(A,9);
cout << "迭代求和结果:" << sum1 << endl;
int sum2 = toSum(A,9);
cout << "递归求和结果:" << sum2 << endl;
myReverse(A,0,8);
cout << "迭代反转数列A为:" << endl;
for(int j=0;j<9;j++)
cout << A[j] <<" ";
cout << "" << endl;
toReverse(A,0,8);
cout << "递归再次反转回数列为:" << endl;
for(int j=0;j<9;j++)
cout << A[j] <<" ";
cout << "" << endl;
cout << "操作结束!" << endl;
return 0;
}
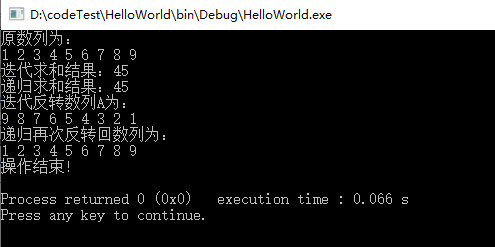
- 控制台输出:
分而治之
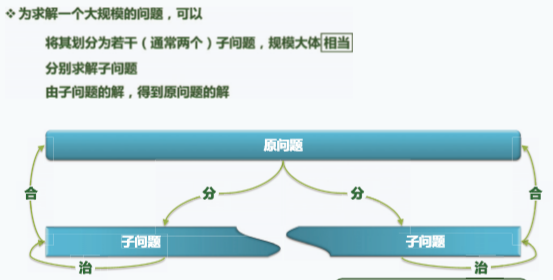
注意和减而治之的区别,两者划分子问题的规模不一致。
- 代码实现:
#include <iostream>
using namespace std;
// 二分递归求和
int binarySum(int a[], int lo, int hi){
if(lo + 1 >= hi) return a[lo];
int mi = (lo + hi) >> 1;
return binarySum(a,lo,mi) + binarySum(a,mi,hi);
}
int main()
{
int A[15]={1,2,3,4,5,6,7,8};
cout << "原数列为:" << endl;
for(int j=0;j<8;j++)
cout << A[j] <<" ";
cout << "" << endl;
// 注意这里的输入区间为(0,n),否则计算会出错
int sum0 = binarySum(A,0,8);
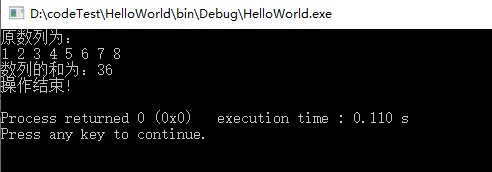
cout << "数列的和为:" <<sum0<<endl;
cout << "操作结束!" << endl;
return 0;
}
- 控制台输出:
相比于之前直接迭代累加,分而治之降低了时间复杂度。
Max2
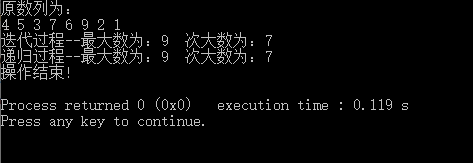
从数组区间中找出最大的两个数。
- 代码实现:
#include <iostream>
using namespace std;
// 迭代找出数组最大两数
void myMax2(int a[], int lo, int hi, int & x1, int & x2){
if(a[x1=lo] < a[x2=lo+1]) swap(x1, x2);
for(int i=lo+2; i<hi; i++){
if(a[x2] < a[i]){
if(a[x1] < a[x2=i])
swap(x1, x2);
}
}
}
// 递归分治找出数组最大两数
void toMax(int a[], int lo, int hi, int & X1, int & X2){
if(hi <= lo+3){myMax2(a, lo, hi, X1, X2); return ;}
int mi = (lo+hi) / 2;
int x1L, x2L; toMax(a, lo, mi, x1L, x2L);
int x1R, x2R; toMax(a, mi, hi, x1R, x2R);
if(a[x1L] > a[x1R]){
X1 = x1L; X2 = a[x2L] > a[x1R] ? x2L : x1R;
}else{X1 = x1R; X2 = a[x2R] > a[x1L] ? x2R : x1L;}
}
int main()
{
int x1,x2,c1,c2;
int A[15]={4,5,3,7,6,9,2,1};
cout << "原数列为:" << endl;
for(int j=0;j<8;j++)
cout << A[j] <<" ";
cout << "" << endl;
// 注意这里区间为(0,n)
myMax2(A,0,8,x1,x2);
cout << "迭代过程--" << "最大数为:" << A[x1] << " 次大数为:" << A[x2] << endl;
// 注意这里区间同样为(0,n)
toMax(A,0,8,c1,c2);
cout << "递归过程--" << "最大数为:" << A[x1] << " 次大数为:" << A[x2] << endl;
cout << "操作结束!" << endl;
return 0;
}
- 控制台输出: